Bubble Sorting

Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order.+

Example

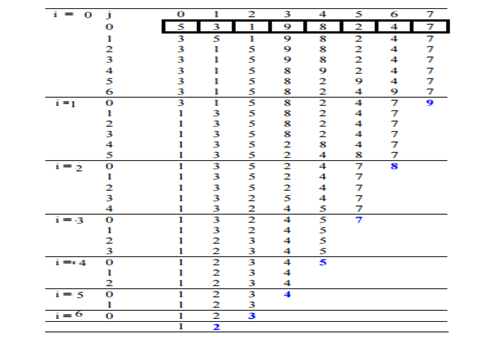
First Pass:
( 51 4 2 8 ) –> ( 15 4 2 8 ), Here, algorithm compares the first two elements, and swaps since 5 > 1.
( 1 54 2 8 ) –>  ( 1 45 2 8 ), Swap since 5 > 4
( 1 4 52 8 ) –>  ( 1 4 25 8 ), Swap since 5 > 2
( 1 4 2 58 ) –> ( 1 4 2 58 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them

Second Pass:
( 14 2 5 8 ) –> ( 14 2 5 8 )
( 1 42 5 8 ) –> ( 1 24 5 8 ), Swap since 4 > 2
( 1 2 45 8 ) –> ( 1 2 45 8 )
( 1 2 4 58 ) –>  ( 1 2 4 58 )

Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.

Third Pass:
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )

ALGORITHM

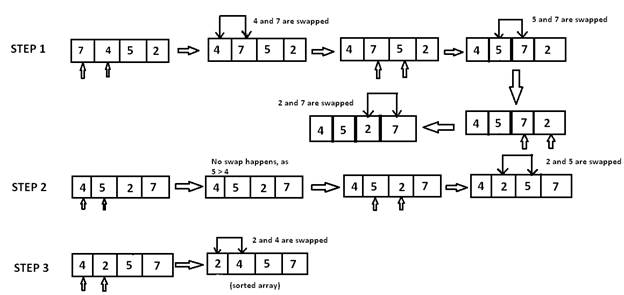
In step 1, 7 is compared with 4. Since 7>4, 7 is moved ahead of 4. Since all the other elements are of a lesser value than 7, 7 is moved to the end of the array.
Now the array is A[]={4,5,2,7}.
Now the array is A[]={4,2,5,7}.
In step 3, the element 4 is compared with 2. Since 4>2 and the elements are in descending order, 4 and 2 are swapped.
The sorted array is A[]={2,4,5,7}.

Time Complexity: 
Worst and Average Case: O(n*n). Worst case occurs when array is reverse sorted.
Best Case: O(n). Best case occurs when array is already sorted.

Auxiliary Space: O(1)

Boundary Cases: Bubble sort takes minimum time (Order of n) when elements are already sorted.
Sorting In Place: Yes
Stable: Yes

Due to its simplicity, bubble sort is often used to introduce the concept of a sorting algorithm.
In computer graphics it is popular for its capability to detect a very small error (like swap of just two elements) in almost-sorted arrays and fix it with just linear complexity (2n). For example, it is used in a polygon filling algorithm, where bounding lines are sorted by their x coordinate at a specific scan line (a line parallel to x axis) and with incrementing y their order changes (two elements are swapped) only at intersections of two lines.

CODE

# Python program for implementation of Bubble Sort 
  
def bubbleSort(arr): 
    n = len(arr) 
  
    # Traverse through all array elements 
    for i in range(n): 
  
        # Last i elements are already in place 
        for j in range(0, n-i-1): 
  
            # traverse the array from 0 to n-i-1 
            # Swap if the element found is greater 
            # than the next element 
            if arr[j] > arr[j+1] : 
                arr[j], arr[j+1] = arr[j+1], arr[j] 
  
# Driver code to test above 
arr = [64, 34, 25, 12, 22, 11, 90] 
  
bubbleSort(arr) 
  
print ("Sorted array is:") 
for i in range(len(arr)): 
    print ("%d" %arr[i])

Output:            Sorted array: 11 12 22 25 34 64 90

# Python3 Optimized implementation 
# of Bubble sort 
  
# An optimized version of Bubble Sort 
def bubbleSort(arr): 
    n = len(arr) 
   
    # Traverse through all array elements 
    for i in range(n): 
        swapped = False
  
        # Last i elements are already 
        #  in place 
        for j in range(0, n-i-1): 
   
            # traverse the array from 0 to 
            # n-i-1. Swap if the element  
            # found is greater than the 
            # next element 
            if arr[j] > arr[j+1] : 
                arr[j], arr[j+1] = arr[j+1], arr[j] 
                swapped = True
  
        
# IF no two elements were swapped 
        # by inner loop, then break 
        if swapped == False: 
            break
           
# Driver code to test above 
arr = [64, 34, 25, 12, 22, 11, 90] 
   
bubbleSort(arr) 
   
print ("Sorted array :") 
for i in range(len(arr)): 
    print ("%d" %arr[i],end=" ")

Output:            Sorted array: 11 12 22 25 34 64 90

Recursive Bubble Sort

Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order.

How to implement it recursively?
Recursive Bubble Sort has no performance/implementation advantages, but can be a good question to check one’s understanding of Bubble Sort and recursion.
If we take a closer look at Bubble Sort algorithm, we can notice that in first pass, we move largest element to end (Assuming sorting in increasing order). In second pass, we move second largest element to second last position and so on.

Recursion Idea.

1. Base Case: If array size is 1, return.
2. Do One Pass of normal Bubble Sort. This pass fixes last element of current subarray.
3. Recur for all elements except last of current subarray.

Time Complexity: Same as regular bubble sort

Auxiliary Space: O(n) for the call stack

CODE

# Python Program for implementation of  
# Recursive Bubble sort 
  
def bubble_sort(listt): 
    for i, num in enumerate(listt): 
        try: 
            if listt[i+1] < num: 
                listt[i] = listt[i+1] 
                listt[i+1] = num 
                bubble_sort(listt) 
        except IndexError: 
            pass
    return listt 
  
listt = [64, 34, 25, 12, 22, 11, 90] 
bubble_sort(listt) 
  
print("Sorted array:"); 
for i in range(0, len(listt)): 
    print(listt[i], end=' ') 

Output:            Sorted array: 11 12 22 25 34 64 90