Pancake sorting

Posted on by Naveen

Given an unsorted array, sort the given array. You are allowed to do only following operation on array.

flip(arr, i): Reverse array from 0 to i

Unlike a traditional sorting algorithm, which attempts to sort with the fewest comparisons possible, the goal is to sort the sequence in as few reversals as possible.
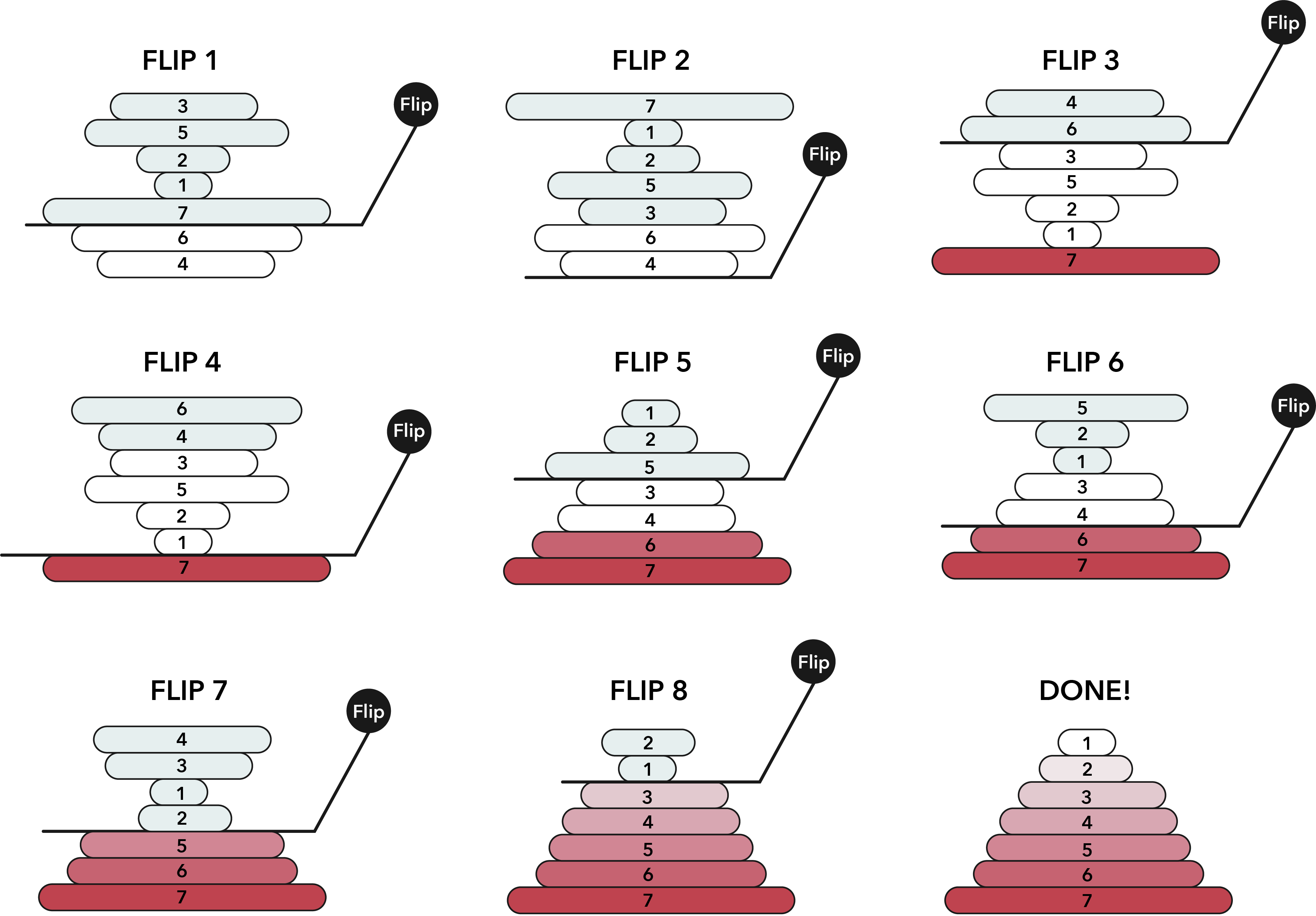
The idea is to do something similar to Selection Sort. We one by one place maximum element at the end and reduce the size of current array by one.

ALGORITHM

Following are the detailed steps. Let given array be arr[] and size of array be n.
1) Start from current size equal to n and reduce current size by one while it’s greater than 1. Let the current size be curr_size. Do following for every curr_size
……a) Find index of the maximum element in arr[0..curr_szie-1]. Let the index be ‘mi’
……b) Call flip(arr, mi)
……c) Call flip(arr, curr_size-1)

Pancake Sorting Input: Stack of pancakes, each of different sizes ...
Pancakes. Sleep. Cocktail. - Kazue Anan - Medium

CODE 

# Python3 program to sort array using pancake sort 
# Reverses arr[0..i] */ 
def flip(arr, i): 
    start = 0
    while start < i: 
        temp = arr[start] 
        arr[start] = arr[i] 
        arr[i] = temp 
        start += 1
        i -= 1
  
# Returns index of the maximum 
# element in arr[0..n-1] */ 
def findMax(arr, n): 
    mi = 0
    for i in range(0,n): 
        if arr[i] > arr[mi]: 
            mi = i 
    return mi 
  
# The main function that  
# sorts given array  
# using flip operations 
def pancakeSort(arr, n): 
      
    # Start from the complete 
    # array and one by one 
    # reduce current size 
    # by one 
    curr_size = n 
    while curr_size > 1: 
        # Find index of the maximum 
        # element in  
        # arr[0..curr_size-1] 
        mi = findMax(arr, curr_size) 
  
        # Move the maximum element 
        # to end of current array 
        # if it's not already at  
        # the end 
        if mi != curr_size-1: 
            # To move at the end,  
            # first move maximum  
            # number to beginning  
            flip(arr, mi) 
  
            # Now move the maximum  
            # number to end by 
            # reversing current array 
            flip(arr, curr_size-1) 
        curr_size -= 1
  
# A utility function to  
# print an array of size n  
def printArray(arr, n): 
    for i in range(0,n): 
        print ("%d"%( arr[i]),end=" ") 
  
# Driver program  
arr = [23, 10, 20, 11, 12, 6, 7] 
n = len(arr) 
pancakeSort(arr, n); 
print ("Sorted Array ") 
printArray(arr,n)

Output:            Sorted Array
6 7 10 11 12 20 23

Time complexity

Total O(n) flip operations are performed in above code. The overall time complexity is O(n^2).

Leave a comment