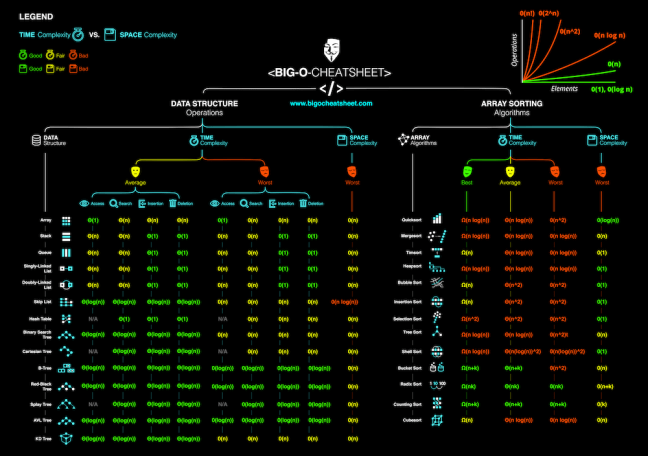
Each data structure has it’s own different way, or different algorithm for sorting, inserting, finding, …etc. This is due to the nature of the data structure. There are algorithms used with specific data structure, where some other can’t be used.

The more efficient & suitable the algorithm, the more you will have an optimized data structure.

Chances are, you’re going to rely on the built-in algorithms used with the data structures in your language. These algorithms are very well optimized and battle tested.

Arrays

Pros

• Easy to create, Easy to use
• Direct indexing: O(1)
• Sequential access: O(N)

Cons

• Sorting: O(NLogN)
• Searching: O(N), and O(LogN) if sorted
• Inserting and deleting: O(N) because of shifting items.

Linked List

Pros

• Inserting and deleting: O(1)
• Sequential Access: O(N)

Inserting and deleting operations refers to the operation itself, as you might need to sequentially access all the nodes until the node you’are looking for.

Inserting and deleting is much easier with doubly linked list.

Cons

• No Direct Access; Only Sequential Access
• Searching: O(N)
• Sorting: O(NLogN)

Stacks and Queues

Stacks and queues have very specific purposes. Stacks are last in, first out data structure (LIFO), while queues are first in, first out (FIFO).

Pros

• Push/Add: O(1)
• Pop/Remove: O(1)
• Peek: O(1)

Cons

If you’re trying to do anything else with stacks or queues, like if you’re asking how can I pull an item from the middle?. Then, you should be looking at a different data structure.

Hash Tables

Pros

• Inserting and deleting: O(1) + Hashing & Indexing (amortized).
• Direct access: O(1) + Hashing & Indexing.

It takes a little processing for the hashing and indexing. But the good thing about that is it’s the same amount of processing every time, even if the hash table gets very large.

When the hash table gets full, it will increase it’s size. And, when the number of filled buckets is much smaller than the size of the hash table, it will then decrease it’s size. Both operations take a complexity of O(N). That’s why insertion and deletion takes O(1) amortized.

Cons

• Some overhead as require a little more space in memory than arrays.
• Retrieval of elements doesn’t guarantee a specific order.
• Searching for a value (without knowing it’s key).

Sets

Pros

• Checking membership; value existence.
• Avoids duplicates

The complexity of checking if a value contained in the set depends on the underlying data structure used to implemented the set.

Cons

Sets are intentionally limited. There aren’t much you can do with them. So, they’re are terrible at almost everything else.

Binary Search Trees (BST)

Pros

• Inserting and deleting
• Speed of Access
• Maintains sorted order; retrieval of elements is in order.

The complexity of insertion, deletion, and accessing would be O(LogN), and O(N) if the tree is unbalanced.

Cons

• Some overhead because of their creation and management.

Heaps

Heaps are a type of binary tree that are great for priority queues.

Pros

• Find Min/Find Max: O(1)
• Inserting: O(LogN)
• Delete Min/Delete Max: O(LogN)

Cons

• Searching and deleting: O(N)

In searching and deleting, we will have to scan all the elements as they don’t guarantee a specific order, unlike BST.

Deleting requires to traverse the whole tree to access the element first, then delete it, where the deletion operation itself requires O(LogN).

Python supported Data structures

Arrays

Support for N-th dimensional arrays is generally built directly into the core language itself. They are index from zero. 

Dynamic Arrays

In Python, list is a data type, just like strings and numbers. It’s an implementation of dynamic arrays.

Linked List

Python does not have a built-in linked list implementation. Python lists are not linked lists, they are dynamic arrays.

Stacks

Python doesn’t have an explicit stack class, but there is a section in the  Python documentation of using lists as stacks.

Queues

The queuemodule offers a queue class. It is especially useful in when working with threading which is very common with queues. It’s also possible to use list as queues , however, lists are not efficient for this purpose.

collections.deque is an alternative implementation of unbounded queues with fast atomic  append() and  popleft() operations that do not require locking.

Deque

Python also has a deque class for this. Even though you could use a Python list, the deque is optimized for this kind of usage; appends and pops on either end.

Priority Queues

Just as a list can be implemented with a linked list or an array, a priority queue can be implemented with a heap  or a variety of other methods.

The queuemodule offers a PriorityQueueclass, which uses heapq module under the hood to prioritize the queue entries. The heapq module uses the heap data structure.
Queue.PriorityQueue is a thread-safe class, while the heapq module makes no thread-safety guarantees.

Dictionaries

In Python, they are called dictionaries. They are implemented as a data type called dict, just like strings and numbers.

Sets

Python supports set and frozenset data types. frozenset is a way of making the set immutable after it has been created.

Graphs

There is no direct support for graph data structure in languages(same as trees). Because the implementation of any graph is always going to be more specific.

For example, A linked list is a kind of graph, a tree is a kind of graph, a heap is a kind of graph. A single linked list would be considered a directed graph, whereas a doubly linked list is a kind of undirected graph. They are all graphs with intentional constraints.

Language/ data Structure	Arrays	Dynamic Arrays	Linked list	Stacks	Queues	Priority Queues	deque	Dictionary	Sets	Graphs
	Built directly into python	list	NA- Python arrays are dynamic arrays not linked list	N/A – Use list as stack instead	queue, deque or use list as queue.	priority queue or heapq	deque	dict	set and frozenset	There is no direct support for graph