Merge Sort

Merge Sort is a Divide and Conquer algorithm. It divides input array in two halves, calls itself for the two halves and then merges the two sorted halves. The merge() function is used for merging two halves. The merge(arr, l, m, r) is key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one.

ALGORITHM:(Divide and Conquer)

MergeSort(arr[], l,  r)
If r > l
     1. Find the middle point to divide the array into two     halves:  
             middle m = (l+r)/2
     2. Call mergeSort for first half:   
             Call mergeSort(arr, l, m)
     3. Call mergeSort for second half:
             Call mergeSort(arr, m+1, r)
     4. Merge the two halves sorted in step 2 and 3:
             Call merge(arr, l, m, r)

Example1:

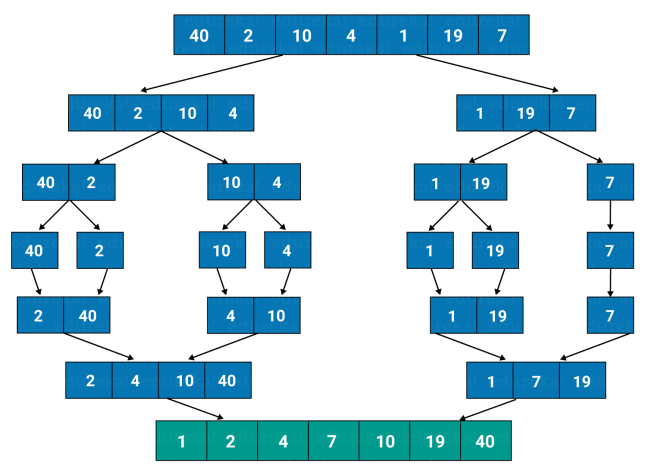
The above diagram shows the complete merge sort process for an example array {38, 27, 43, 3, 9, 82, 10}. If we take a closer look at the diagram, we can see that the array is recursively divided in two halves till the size becomes 1. Once the size becomes 1, the merge processes comes into action and starts merging arrays back till the complete array is merged.

CODE

# Python program for implementation of MergeSort 
def mergeSort(arr): 
    if len(arr) >1: 
        mid = len(arr)//2 #Finding the mid of the array 
        L = arr[:mid] # Dividing the array elements  
        R = arr[mid:] # into 2 halves 
  
        mergeSort(L) # Sorting the first half 
        mergeSort(R) # Sorting the second half 
  
        i = j = k = 0
          
        # Copy data to temp arrays L[] and R[] 
        while i < len(L) and j < len(R): 
            if L[i] < R[j]: 
                arr[k] = L[i] 
                i+=1
            else: 
                arr[k] = R[j] 
                j+=1
            k+=1
          
        # Checking if any element was left 
        while i < len(L): 
            arr[k] = L[i] 
            i+=1
            k+=1
          
        while j < len(R): 
            arr[k] = R[j] 
            j+=1
            k+=1
  
# Code to print the list 
def printList(arr): 
    for i in range(len(arr)):         
        print(arr[i],end=" ") 
    print() 
  
# driver code to test the above code 
if __name__ == '__main__': 
    arr = [12, 11, 13, 5, 6, 7]  
    print ("Given array is", end="\n")  
    printList(arr) 
    mergeSort(arr) 
    print("Sorted array is: ", end="\n") 
    printList(arr) 

Output:           Given array is
12 11 13 5 6 7
Sorted array is
5 6 7 11 12 13

Time Complexity:

Sorting arrays on different machines. Merge Sort is a recursive algorithm and time complexity can be expressed as following recurrence relation.
T(n) = 2T(n/2) + θ(n)
The above recurrence can be solved either using Recurrence Tree method or Master method. It falls in case II of Master Method and solution of the recurrence is θ(nLogn).
Time complexity of Merge Sort is θ(nLogn) in all 3 cases (worst, average and best) as merge sort always divides the array into two halves and take linear time to merge two halves.

Auxiliary Space: O(n)

Algorithmic Paradigm: Divide and Conquer
Sorting In Place: No in a typical implementation
Stable: Yes
Online: Yes

Output:           Given array is
12 11 13 5 6 7
Sorted array is
5 6 7 11 12 13

Uses:
1.Merge Sort is useful for sorting linked lists in O(nLogn) time.In the case of linked lists, the case is different mainly due to the difference in memory allocation of arrays and linked lists. Unlike arrays, linked list nodes may not be adjacent in memory. Unlike an array, in the linked list, we can insert items in the middle in O(1) extra space and O(1) time. Therefore merge operation of merge sort can be implemented without extra space for linked lists. In arrays, we can do random access as elements are contiguous in memory. Let us say we have an integer (4-byte) array A and let the address of A[0] be x then to access A[i], we can directly access the memory at (x + i*4). Unlike arrays, we can not do random access in the linked list. Quick Sort requires a lot of this kind of access. In linked list to access i’th index, we have to travel each and every node from the head to i’th node as we don’t have a continuous block of memory. Therefore, the overhead increases for quicksort. Merge sort accesses data sequentially and the need of random access is low.
2. Inversion Count Problem
3. Used in External Sorting

Recursive Merge Sort

# Recursive Python Program for merge sort 
  
def merge(left, right): 
    if not len(left) or not len(right): 
        return left or right 
  
    result = [] 
    i, j = 0, 0
    while (len(result) < len(left) + len(right)): 
        if left[i] < right[j]: 
            result.append(left[i]) 
            i+= 1
        else: 
            result.append(right[j]) 
            j+= 1
        if i == len(left) or j == len(right): 
            result.extend(left[i:] or right[j:]) 
            break 
  
    return result 
  
def mergesort(list): 
    if len(list) < 2: 
        return list
  
    middle = len(list)/2
    left = mergesort(list[:middle]) 
    right = mergesort(list[middle:]) 
  
    return merge(left, right) 
      
seq = [12, 11, 13, 5, 6, 7] 
print("Given array is") 
print(seq);  
print("\n") 
print("Sorted array is") 
print(mergesort(seq))

Output:           Given array is
12 11 13 5 6 7
Sorted array is
5 6 7 11 12 13

Iterative Merge Sort

The above function is recursive, so uses function call stack to store intermediate values of l and h. The function call stack stores other bookkeeping information together with parameters. Also, function calls involve overheads like storing activation record of the caller function and then resuming execution. Unlike Iterative QuickSort, the iterative MergeSort doesn’t require explicit auxiliary stack.
The above function can be easily converted to iterative version. Following is iterative Merge Sort.

# Iterative Merge sort (Bottom Up) 
  
# Iterative mergesort function to 
# sort arr[0...n-1]  
def mergeSort(a): 
      
    current_size = 1
      
    # Outer loop for traversing Each  
    # sub array of current_size 
    while current_size < len(a) - 1: 
          
        left = 0
        # Inner loop for merge call  
        # in a sub array 
        # Each complete Iteration sorts 
        # the iterating sub array 
        while left < len(a)-1: 
              
            # mid index = left index of  
            # sub array + current sub  
            # array size - 1 
            mid = left + current_size - 1
              
            # (False result,True result) 
            # [Condition] Can use current_size 
            # if 2 * current_size < len(a)-1 
            # else len(a)-1 
            right = ((2 * current_size + left - 1, 
                    len(a) - 1)[2 * current_size  
                          + left - 1 > len(a)-1]) 
                            
            # Merge call for each sub array 
            merge(a, left, mid, right) 
            left = left + current_size*2
              
        # Increasing sub array size by 
        # multiple of 2 
        current_size = 2 * current_size 
  
# Merge Function 
def merge(a, l, m, r): 
    n1 = m - l + 1
    n2 = r - m 
    L = [0] * n1 
    R = [0] * n2 
    for i in range(0, n1): 
        L[i] = a[l + i] 
    for i in range(0, n2): 
        R[i] = a[m + i + 1] 
  
    i, j, k = 0, 0, l 
    while i < n1 and j < n2: 
        if L[i] > R[j]: 
            a[k] = R[j] 
            j += 1
        else: 
            a[k] = L[i] 
            i += 1
        k += 1
  
    while i < n1: 
        a[k] = L[i] 
        i += 1
        k += 1
  
    while j < n2: 
        a[k] = R[j] 
        j += 1
        k += 1
  
  
# Driver code 
a = [12, 11, 13, 5, 6, 7] 
print("Given array is ") 
print(a) 
  
mergeSort(a) 
  
print("Sorted array is ") 
print(a) 

Output:           Given array is
12 11 13 5 6 7
Sorted array is
5 6 7 11 12 13

Time Complexity: O(nLogn)