Kadane’s algorithm – (Largest Sum Contiguous Sub-array)

Kadane’s algorithm is to look for all positive contiguous segments of the array (max_ending_here is used for this). And keep track of maximum sum contiguous segment among all positive segments (max_so_far is used for this). Each time we get a positive sum compare it with max_so_far and update max_so_far if it is greater than max_so_far

Insertion sort is a simple sorting algorithm that works the way we sort playing cards in our hands.

ALGORITHM

Initialize:
max_so_far = 0
max_ending_here = 0

Loop for each element of the array
(a) max_ending_here = max_ending_here + a[i]
(b) if(max_ending_here < 0)
max_ending_here = 0
(c) if(max_so_far < max_ending_here)
max_so_far = max_ending_here
return max_so_far

Example:

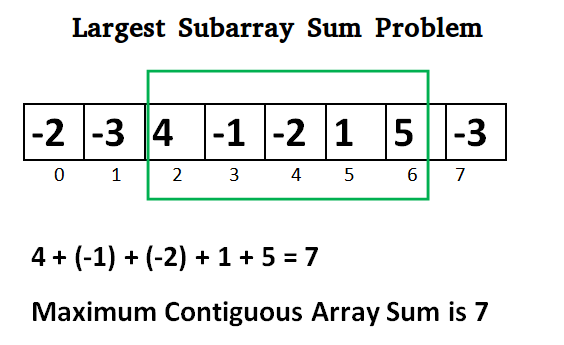
    Lets take the example:
    {-2, -3, 4, -1, -2, 1, 5, -3}

    max_so_far = max_ending_here = 0

    for i=0,  a[0] =  -2
    max_ending_here = max_ending_here + (-2)
    Set max_ending_here = 0 because max_ending_here < 0

    for i=1,  a[1] =  -3
    max_ending_here = max_ending_here + (-3)
    Set max_ending_here = 0 because max_ending_here < 0

    for i=2,  a[2] =  4
    max_ending_here = max_ending_here + (4)
    max_ending_here = 4
    max_so_far is updated to 4 because max_ending_here greater 
    than max_so_far which was 0 till now

    for i=3,  a[3] =  -1
    max_ending_here = max_ending_here + (-1)
    max_ending_here = 3

    for i=4,  a[4] =  -2
    max_ending_here = max_ending_here + (-2)
    max_ending_here = 1

    for i=5,  a[5] =  1
    max_ending_here = max_ending_here + (1)
    max_ending_here = 2

    for i=6,  a[6] =  5
    max_ending_here = max_ending_here + (5)
    max_ending_here = 7
    max_so_far is updated to 7 because max_ending_here is 
    greater than max_so_far

    for i=7,  a[7] =  -3
    max_ending_here = max_ending_here + (-3)
    max_ending_here = 4

PROBLEM

Given an integer array , find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6

CODE

# Function to find the maximum contiguous subarray 
  
def max_output(arr):
    max_so_far = 0
    max_ending_here = 0
    for i in range(len(arr)):
        max_ending_here += arr[i]

        if max_ending_here < 0:
            max_ending_here = 0
        elif max_so_far < max_ending_here:
            max_so_far = max_ending_here
    return max_so_far
    
arr=[-2,1,-3,4,-1,2,1,-5,4]        
max_output(arr)

Time Complexity: O(n)