Jump Search

The basic idea is to check fewer elements (than linear search) by jumping ahead by fixed steps or skipping some elements in place of searching all elements.

Important points

• Works only sorted arrays.
• The optimal size of a block to be jumped is (√ n). This makes the time complexity of Jump Search O(√ n).
• The time complexity of Jump Search is between Linear Search ((O(n)) and Binary Search (O(Log n)).
• Binary Search is better than Jump Search, but Jump search has an advantage that we traverse back only once (Binary Search may require up to O(Log n) jumps, consider a situation where the element to be searched is the smallest element or smaller than the smallest). So in a system where binary search is costly, we use Jump Search.

What is the optimal block size to be skipped?
In the worst case, we have to do n/m jumps and if the last checked value is greater than the element to be searched for, we perform m-1 comparisons more for linear search. Therefore the total number of comparisons in the worst case will be ((n/m) + m-1). The value of the function ((n/m) + m-1) will be minimum when m = √n. Therefore, the best step size is m = √n.

APPROACH

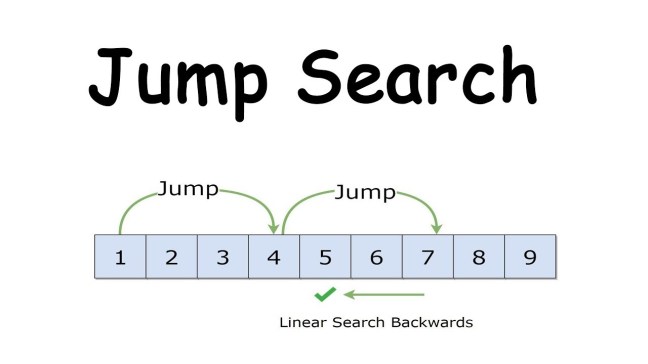
For example, suppose we have an array arr[] of size n and block (to be jumped) size m. Then we search at the indexes arr[0], arr[m], arr[2m]…..arr[km] and so on. Once we find the interval (arr[km] < x < arr[(k+1)m]), we perform a linear search operation from the index km to find the element x.
Let’s consider the following array: (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610). Length of the array is 16. Jump search will find the value of 55 with the following steps assuming that the block size to be jumped is 4.
STEP 1: Jump from index 0 to index 4.
STEP 2: Jump from index 4 to index 8.
STEP 3: Jump from index 8 to index 12.
STEP 4: Since the element at index 12 is greater than 55 we will jump back
a step to come to index 8.
STEP 5: Perform linear search from index 8 to get the element 55.

CODE

import math 
  
def jumpSearch( arr , x , n ): 
      
    # Finding block size to be jumped 
    step = math.sqrt(n) 
      
    # Finding the block where element is 
    # present (if it is present) 
    prev = 0
    while arr[int(min(step, n)-1)] < x: 
        prev = step 
        step += math.sqrt(n) 
        if prev >= n: 
            return -1
      
    # Doing a linear search for x in  
    # block beginning with prev. 
    while arr[int(prev)] < x: 
        prev += 1
          
        # If we reached next block or end  
        # of array, element is not present. 
        if prev == min(step, n): 
            return -1
      
    # If element is found 
    if arr[int(prev)] == x: 
        return prev 
      
    return -1
  
# Driver code to test function 
arr = [ 0, 1, 1, 2, 3, 5, 8, 13, 21, 
    34, 55, 89, 144, 233, 377, 610 ] 
x = 55
n = len(arr) 
  
# Find the index of 'x' using Jump Search 
index = jumpSearch(arr, x, n) 
  
# Print the index where 'x' is located 
print("Number" , x, "is at index" ,"%.0f"%index) 

Output:                Number 55 is at index 10